USACO Guide: Moocast

The Problem
The problem text is shown below (USACO Page):

Explanation
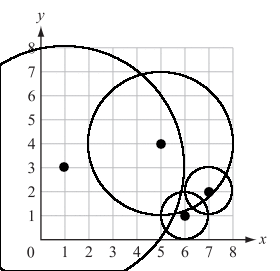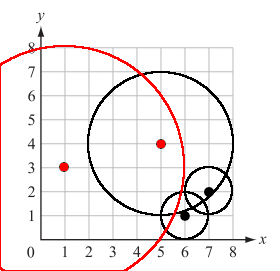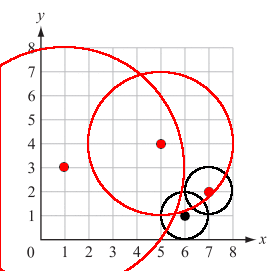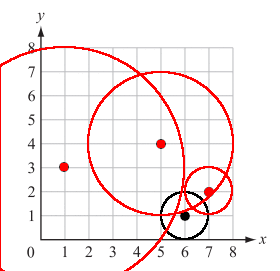
Sometimes, creating a visual for a problem can give you all the insight you need to solve it. When I saw this problem, the first thing I did was draw out the sample case. I started with the sample case: I made myself a coordinate grid, plotted out the points, and drew the ranges of the walkie-talkies as circles, with the given power of each walkie-talkie as the circle’s radius. This is what my diagram looked like:
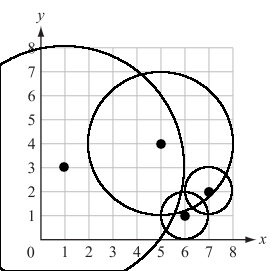
I then ran through the process in my head, counting out how many cows received the message with each cow as a starting point. I did not skip steps and ran through it as I imagined an algorithm would, giving me the following process for the solution (a signal starting at cow 1 that reaches 3 cows):
As you may have noticed while watching the signal spread, it did so in such a way that was very similar to the well-known algorithm of Breadth-first search (hereafter BFS). Here is a diagram demonstrating BFS applied to a tree:
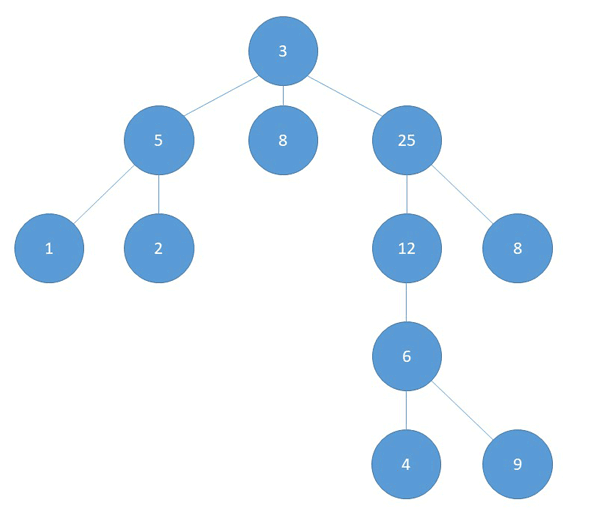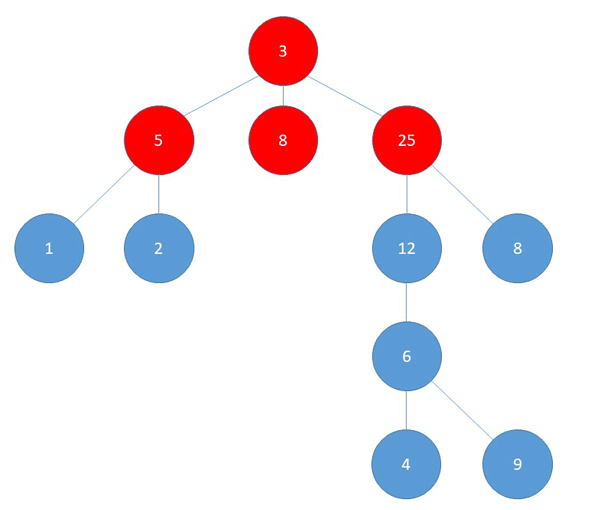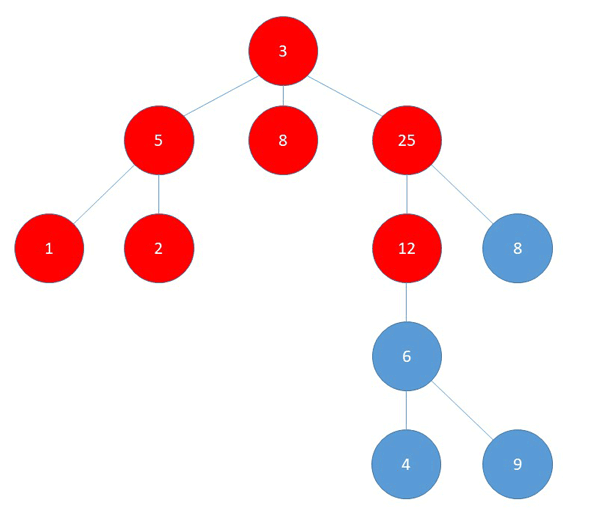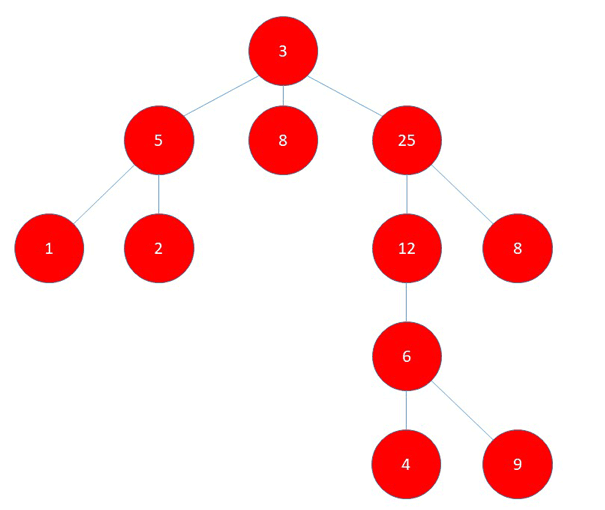
How are the two similar? Both begin at one root point, then spread to all unvisited adjacent nodes (or cows) in the tree before spreading further down the line. Thus, I decided to implement a BFS algorithm to obtain my solution. More specifically, I decided to run a BFS from every cow, keeping track of the number of cows reached by a signal from that cow. In the end, the largest number of cows reached by any BFS (signal) would be my solution.
I implemented this in my code through the common technique of storing a tree through the form of an adjacency list, and I initialized this list once before beginning any BFS by looping through every possible pair of cows, checking which, if any, of the cows could reach the other, and then adding to their adjacency Lists correspondingly. All that was left was to implement a BFS (I worried about recursion’s impact on memory, so I just used a Queue) and keep track of the largest number of cows reached by any one signal. There are plenty of comments in my code, so I will not go through it chunk by chunk and explain what is happening as I have in some previous posts.
My Solution
import java.io.*;
import java.util.*;
public class Moocast {
private static String fileNamePrefix = "moocast";
public static void main(String[] args) throws IOException {
BufferedReader reader = new BufferedReader(new FileReader(fileNamePrefix + ".in"));
StringTokenizer stringTokenizer = new StringTokenizer(reader.readLine());
int[][] cows = new int[Integer.parseInt(stringTokenizer.nextToken())][3];
for (int i = 0; i < cows.length; i++) {
stringTokenizer = new StringTokenizer(reader.readLine());
// cowData = [x, y, radius of broadcast]
int[] cowData = {Integer.parseInt(stringTokenizer.nextToken()), Integer.parseInt(stringTokenizer.nextToken()), Integer.parseInt(stringTokenizer.nextToken())};
cows[i] = cowData;
}
reader.close();
// Represent the tree as adjacency lists (an array of List<Integer>s of cows in range)
List<Integer>[] adjacencies = new List[cows.length];
// Initialize the lists for each cow
for (int i = 0; i < adjacencies.length; i++)
adjacencies[i] = new ArrayList<>();
// Loop through every cow and set up the adjacency lists
for (int cowOne = 0; cowOne < cows.length; cowOne++)
for (int cowTwo = cowOne + 1; cowTwo < cows.length; cowTwo++) {
if (isWithinRange(cows[cowOne], cows[cowTwo]))
adjacencies[cowOne].add(cowTwo);
if (isWithinRange(cows[cowTwo], cows[cowOne]))
adjacencies[cowTwo].add(cowOne);
}
// Perform a BFS from each cow and find the longest BFS length
int maxBroadcast = 0;
for (int cow = 0; cow < cows.length; cow++) {
// Visited array to ensure we don't check or count the same cow twice
boolean[] visited = new boolean[cows.length];
// BFS path length for cow
int broadcastStrength = 0;
// Queue of cows to check
Queue<Integer> queue = new LinkedList<>();
queue.add(cow);
visited[cow] = true;
while (!queue.isEmpty()) {
int currentCow = queue.poll(); // Get the cow at the top of the queue
visited[currentCow] = true;
broadcastStrength++; // This cow has been reached, increase the number of cows in this broadcast
// Add all adjacent cows to the end of the queue
for (int connectedCow : adjacencies[currentCow])
if (!visited[connectedCow]) {
queue.add(connectedCow);
visited[connectedCow] = true;
}
}
// Update the current maximum broadcast strength
maxBroadcast = Math.max(maxBroadcast, broadcastStrength);
}
PrintWriter writer = new PrintWriter(new BufferedWriter(new FileWriter(fileNamePrefix + ".out")));
writer.println(maxBroadcast);
writer.close();
}
// Are the x and y coordinates of otherCow inside the circle around thisCow?
private static boolean isWithinRange(int[] thisCow, int[] otherCow) {
// Uses the Pythagorean Theorem to determine the distance between the center of the thisCow circle and otherCow
double distanceSquared = Math.pow(thisCow[0] - otherCow[0], 2) + Math.pow(thisCow[1] - otherCow[1], 2);
// If otherCow is in the circle, this distance squared must be less than the radius squared
return distanceSquared <= Math.pow(thisCow[2], 2);
}
}
Results
This solution successfully passes all test cases without exceeding the memory or runtime limits, as seen below:
